Good ideas and conversation. No ads, no tracking. Login or Take a Tour!
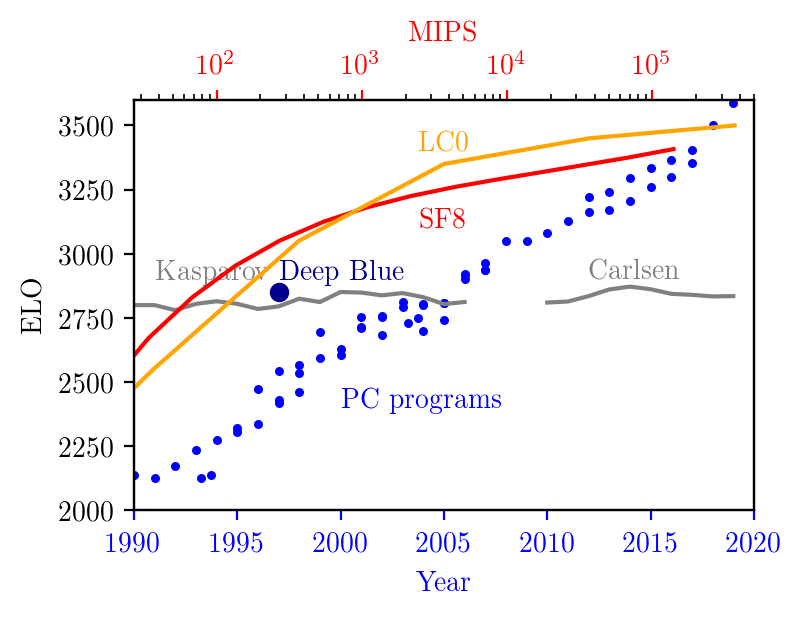
- How can we measure a potential AI or hardware overhang? For the problem of chess, modern algorithms gained two orders of magnitude in compute (or ten years in time) compared to older versions. While it took the supercomputer "Deep Blue" to win over world champion Gary Kasparov in 1997, today's Stockfish program achieves the same ELO level on a 486-DX4-100 MHz from 1994.
- The gray line shows the ELO rating of Kasparov and Carlsen over time, hovering around 2800. The blue symbols indicate the common top engines at their times. The plot is linear in time, and logarithmic in compute. Consequently, ELO scales approximately with the square of compute. Finally, the red line shows the ELOs of SF8 as a function of compute. Starting with the 2019 rating of ~3400 points, it falls below 3000 when reducing MIPs from 10^5 to a few times 10^3. This is a decrease of 2-3 orders of magnitude. It falls below 2850 ELO, Kasparov's level, at 68 MIPs. For comparison, the 486 achieves 70 MIPS at 100 MHz. At its maximum, the hardware overhang amounts to slightly more than 10 years in time, or 2-3 orders of magnitude in compute.
user-inactivated · 1542 days ago · link ·
> In principle, it would be very interesting to make this work: Train a network on today's machines, and execute (run) it on a very old (slow) machine. We do something similar all the time: train networks in the cloud and convert the resulting model to run on mobile devices. To be honest, the classical chess engine is an expert system, which aren't really the current direction of the field and so probably aren't going to tell you that much about future hardware-software tradeoffs. For example, although the article says he used a 2020 chess engine, he used SF8 which is from 2016, and the current version (12) uses a NN-based approach which apparently beats the previous version 10 to 1.